扑克中的数学，loat变成了强听牌，天选之人还是素材集锦？

Float（缠打）是一种比较进阶的扑克策略，其概念是在某一条街拿着几乎完全没有胜率的牌跟注对方下注，并希望在下一条街通过下注拿下底池的策略。常见的float打法是在flop有利位置跟注一个翻牌持续下注过多的玩家，当对手在turn上示弱时，争取通过转牌的下注拿下底池；如果对手继续开枪，那我们就放弃这个底池。但当我们的缠打缠着缠着成为了一手强听牌时，我们似乎就面临了一个窘境。原先的计划是对手如果在转牌继续开枪，我们就果断弃掉我们的垃圾牌；然而，当我们的牌有了不少的outs时，似乎弃牌显得相当可惜了。

所以我们到底应该如何处理这种情况呢？我们将在之后的几章专栏中持续地探讨这个问题。今天我们处理的是对手可能拿着中等牌力手牌的情况。

以这个道友的牌例为例，flop是Js8h2h，hero手持6s7s缠打，转牌9s，帮助hero形成combo draw，有多达15张的outs。这里我们姑且认为对手的手牌是两条街价值的成手牌，类似AJ、J8（甚至超对）这样的牌力，在河牌对手会选择过牌，并会考虑是否跟注hero的下注，那么此时hero与villain博弈的均衡点是什么样的呢？

首先明确下hero的策略，他在转牌可以弃牌（EV是0），而如果他跟注的话，河牌必须要在某些没听到牌的时候选择诈唬（否则对手可以选择永远不跟注他河牌的价值下注，而他在转牌的胜率又不足以支撑其底池赔率，这样他长期肯定是负EV的）。那么villain的策略就很简单了，他会以一定的概率在河牌选择跟注对手。

现在我们来设定所有的参数：转牌的pot大小为p，hero在转牌需要跟注的量为tp，其胜率为q，而河牌hero的bet大小为xp（不管是价值下注还是诈唬），河牌对手的弃牌率为a，而hero河牌下注中诈唬比例为b。

我们画一个树形图来表达一下这个博弈的过程：

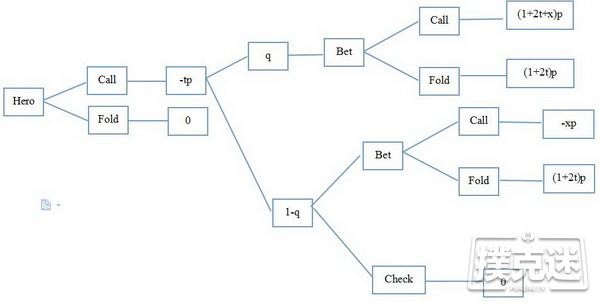
如上图所示，我们可以得到许多均衡点。

首先，当hero河牌没有成牌时，他放弃底池的收益为0，而他下注的收益是a(1+2t)p-xp(1-a)。而为了使hero下注与否是无差异的，villain必然会令hero下注的收益也是0。因此，我们有a(1+2t)p-xp(1-a)=0，可以得到a=x/(1+2t+x)。

其次，villain在河牌弃牌的收益是0，跟注的收益是b(1+2t+x)p-xp(1-b)。为了使villain在河牌call与不call是无差异的，hero必然会使得villain跟注的收益也是0。因此，我们有b(1+2t+x)p-xp(1-b)=0，可以得到b=x/(1+2t+2x)。

最后，我们可以得到hero整个跟注策略的总EV：q(1-a)(1+2t+x)p+qa(1+2t)p-tp，其中，a=x/(1+2t+x)。而他直接弃牌的EV是0，那么，求解方程q(1-a)(1+2t+x)p+qa(1+2t)p-tp=0即可得到我们所想得到的x值。

我们用一个excel图表来更清晰地看这个方程的意义。

为了方便起见，我们统一设定p=1。在本例中，q=0.3，t=1/2，对x采用穷举法，如图所示：

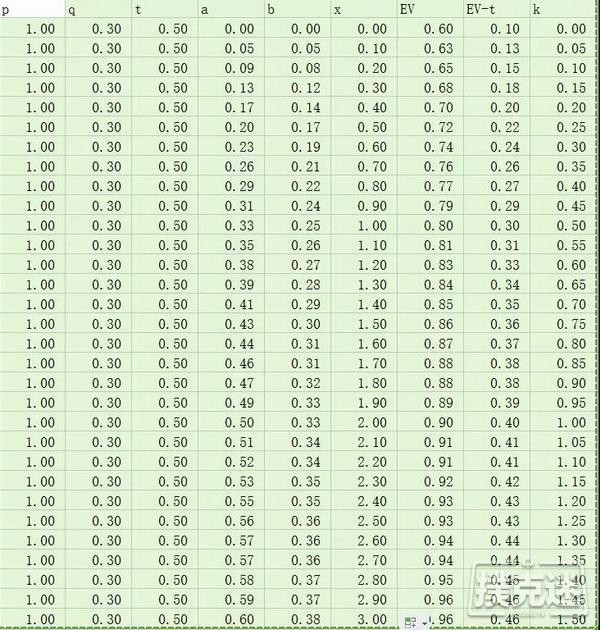
我们会发现，在有如此高的胜率的情况下，跟注几乎总是正EV的选择。

而如果对胜率进行调整，如至0.20，我们会发现hero必须要在河牌攫取一定的价值才可以保持平衡：

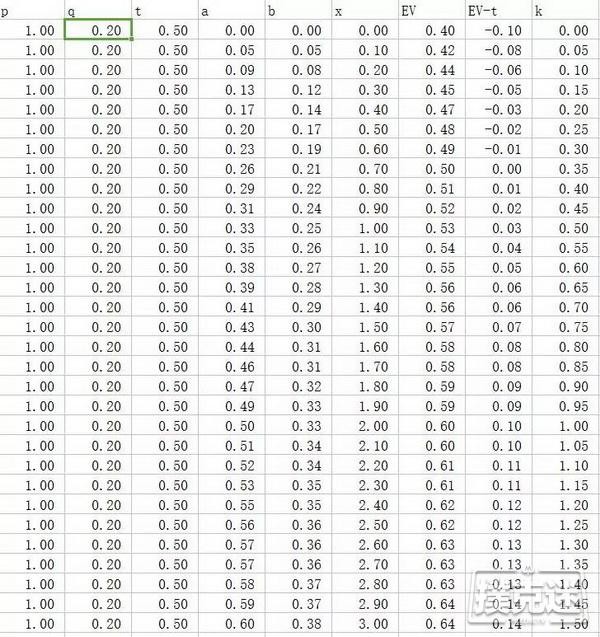
而当胜率变为0.16时，获取正EV的条件忽然就变得相当苛刻了，我们要完成一个超pot下注才能挽回我们的损失，同时要求对手有接近50%的弃牌率：

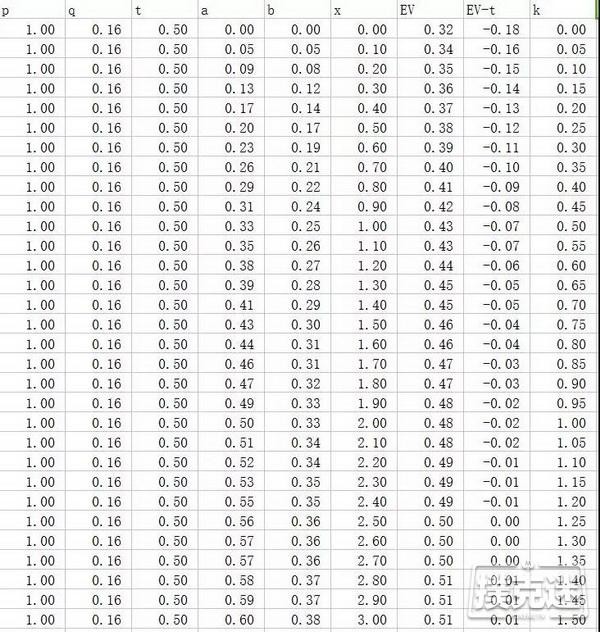
而改变转牌对手下注的大小也会使得我们平衡的条件变化，如果提升t至3/4，我们会发现就算有20%的胜率，跟注也很难有什么价值了：

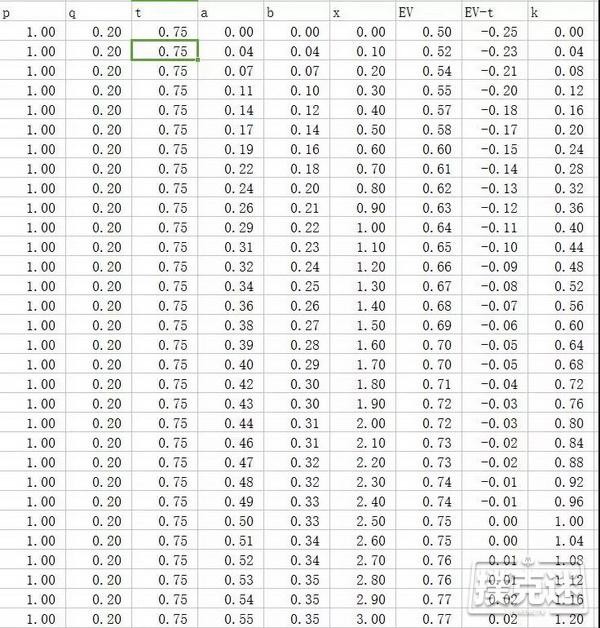
而当t值变为1时，胜率0.25的情况还是可以保持收益的，只要你在河牌能打一个半pot以上的注码，而对手弃牌率可以达到1/3即可，看起来并不那么困难。

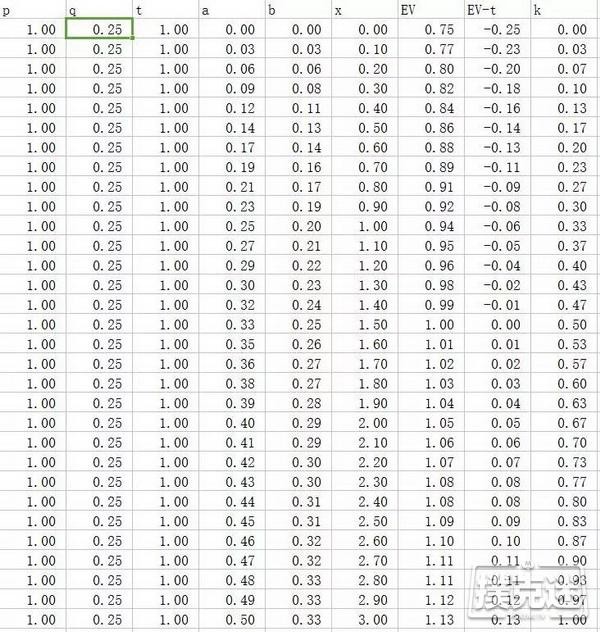
而这么看来，本例中的0.30的胜率真的是很难不盈利啊！看起来我们这位道友的想法有点想当然了！